la
admitancia de un circuito es la facilidad que este ofrece al paso de la corriente. Fue Oliver Heaviside quien comenzó a emplear este término en diciembre de 1887.
De acuerdo con su definición, la admitancia 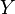 es la inversa de la impedancia,
es la inversa de la impedancia,  :
:

En el SI, la unidad de la admitancia es el Siemens, también llamada mho, proveniente de la unidad de resistencia, ohm, a la inversa.
Al igual que la impedancia, la admitancia se puede considerar cuantitativamente como un valor complejo:

esto es, su módulo es el inverso del módulo de la impedancia y su argumento el de ésta cambiado de sígno.
Si utilizamos la forma binómica de  :
:

Multiplicando numerador y denominador por "R - Xj" y operando resulta:

Expresión que permite definir las componentes real e imaginaria de la admitancia en función de los valores resistivo, R, y reactivo, X, de la impedancia:


Luego,

A G se la denomina conductancia y a B susceptancia.
Si fueran conocidas las componetes G y B de la admitancia, y a partir de ellas se quieren determinar los valore de R y X de la impedancia, puede demostrarse que:


En los análisis de circuitos en paralelo se suele utilizar la admitancia en lugar de la impedancia para simplificar los cálculos.